Módulos
Cuando un diseño ha sido compuesto por una cantidad de formas, las idénticas o similares entre sí son «formas unitarias» o «módulos» que aparecen más de una vez en el diseño.
La presencia de módulos tiende a unificar el diseño. Los módulos pueden ser descubiertos fácilmente en casi todos los diseños si los buscamos. Un diseño puede contener más de un conjunto de módulos.
Los módulos deben ser simples. Los demasiado complicados tienden a destacarse como formas individuales, con lo que el efecto de unidad puede ser anulado.
Repetición de módulos
Si utilizamos la misma forma más de una vez en un diseño, la utilizamos en repetición.
La repetición es el método más simple para el diseño. Las columnas y las ventanas en arquitectura, las patas de un mueble, el dibujo sobre una tela, las baldosas de un suelo, son ejemplos obvios de la repetición.
La repetición de módulos suele aportar una inmediata sensación de armonía. Cada módulo que se repite es como el compás de un ritmo dado. Cuando los módulos son utilizados en gran tamaño y pequeñas cantidades, el diseño puede parecer simple y audaz; cuando son infinitamente pequeños y se utilizan en grandes cantidades, el diseño puede parecer un ejemplo de textura uniforme, compuesto de diminutos elementos.
Tipos de repetición
Con una idea precisa, la repetición debe ser considerada respecto a cada uno de los elementos visuales y de relación:
a) Repetición de figura. La figura es siempre el elemento más importante. Las figuras que se repiten pueden tener diferentes medidas, colores, etc (fig 13a)
b) Repetición de tamaño. La repetición de tamaño sólo es posible cuando las figuras son también repetidas o muy similares (fig. 13b).
c) Repetición de color. Esto supone que todas las formas tienen el mismo color, pero que sus figuras y tamaños pueden variar (fig. 13c).
d) Repetición de textura. Todas las formas pueden ser de la misma textura, pero pueden ser de diferentes conformaciones, medidas o colores. En la impresión, todas las formas sólidamente impresas con la misma clase de tinta sobre la misma superficie son consideradas de una misma textura (fig. 13d).
e) Repetición de dirección. Esto sólo es posible cuando las formas muestran un sentido definido de dirección, sin la menor ambigüedad (fig. 13e).
f) Repetición de posición. Esto se refiere a cómo se disponen las formas, de acuerdo a una estructura.
g) Repetición de espacio. Todas las formas pueden ocupar su espacio de una misma manera. En otras palabras, pueden ser todas positivas, o todas negativas, o relacionadas de la misma manera con el plano de la imagen.
h) Repetición de gravedad. La gravedad es un elemento demasiado abstracto para ser utilizado repetidamente. Es dificultoso afirmar que las formas sean de igual pesantez o liviandad, de igual estabilidad o inestabilidad, a menos que todos los otros elementos estén en estricta repetición.

Variaciones de la repetición
La repetición de todos los elementos puede resultar monótona. La repetición de un solo elemento puede no provocar la sensación de orden y de armonía que asociamos normalmente con la disciplina de la repetición. Si la mayor parte de los elementos visuales están en repetición, deben explorarse las posibilidades de variaciones direccionales o espaciales.
Variaciones direccionales
Con la excepción del círculo, todas las formas pueden variar de dirección en cierto grado. Aun los círculos pueden ser agrupados para dar una sensación de dirección. Pueden distinguirse varias clases de arreglos direccionales:.
a) Direcciones repetidas (fig. 14a).
b) Direcciones indefinidas (fig. 14b).
c) Direcciones alternadas (fig. 14c).
d) Direcciones en gradación (fig. 14d).
e) Direcciones similares (fig. 14e).

Variaciones espaciales
Éstas pueden ser obtenidas reuniendo a las formas en una cantidad de interrelaciones, como vimos anteriormente. Las direcciones repetidas y las dispuestas en forma más regular pueden ser mezcladas con algunas direcciones irregulares. El uso imaginativo de la superposición, la penetración, la unión o las combinaciones y negativas puede conducir a resultados sorprendentes.
Submódulos y supermódulos
Un módulo puede estar compuesto por elementos más pequeños, que son utilizados en repetición. Tales elementos más pequeños son denominados submódulos».
Si los módulos, al ser organizados en un diseño, se agrupan juntos para convertirse en una forma mayor, que luego es utilizada en repetición, denominamos «supermódulos» a estas formas mayores o nuevas. Los supermódulos pueden ser utilizados en un diseño junto a módulos comunes si así fuera necesario.
Tal como podemos tener más de un solo tipo de módulos, podemos tener también, si así se desea, una variedad de supermódulos.
El encuentro de los cuatro círculos
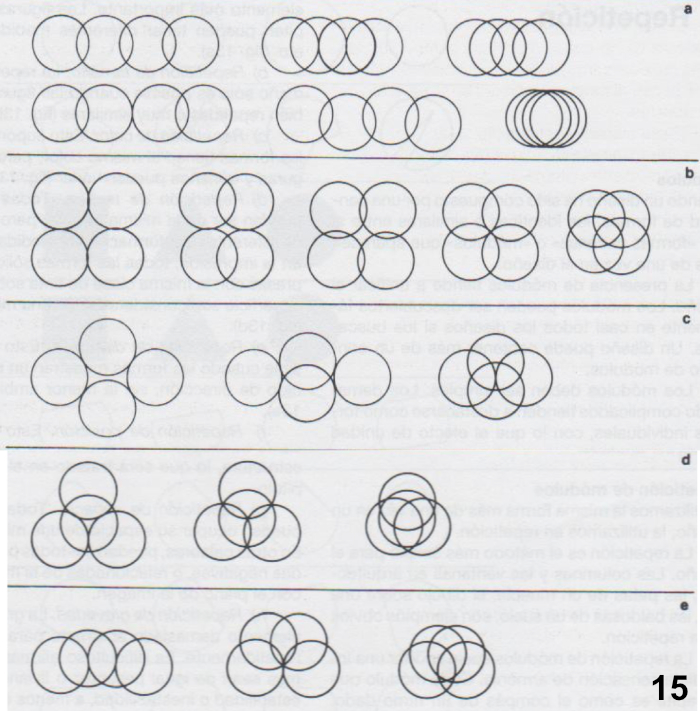
Para ilustrar la formación de supermódulos, vemos como pueden agruparse cuatro círculos del mismo tamaño. Las posibilidades son claramente ilimitadas. pero podemos examinar algunas de las formas más comunes de disposición:
a) Disposición lineal. Los circuios son alineados como si fueran guiados por una línea conceptual que pasara por los centros de todos los círculos. La línea conceptual puede ser recta, curva oquebrada. La distancia entre los círculos puede ser regulada como se desee. Nótese, en un caso extremo, que cada uno de los círculos cruza simultáneamente sobre los otros tres, produciendo hasta trece divisiones (fig. 15a).
b) Disposición cuadrada o rectangular. En este caso los cuatro círculos ocupan cuatro puntos que, entre sí, pueden formar un cuadrado o un rectángulo. Igual que en el caso a), se produce un caso extremo que muestra trece divisiones cuando todos los círculos se penetran profundamente entre sí (fig. 15b).
c) Disposición en rombo. Aquí los cuatro círculos ocupan cuatro puntos que, unidos entre sí, pueden formar un rombo. Regulando la distancia entre los círculos, pueden surgir varios tipos de supermódulos (fig. 15c).
d) Disposición triangular. Aquí los cuatro círculos son dispuestos para que tres de ellos ocupen los tres extremos de un triángulo, con el cuarto en el centro. Esto produce también interesantes supermódulos (fig. 15d).
e) Disposición circular. Cuatro círculos en disposición circular producen el mismo resultado que en la disposición cuadrada, pero la disposición circular puede ser muy singular agregando más círculos. Cuatro circuios pueden ser dispuestos para sugerir un arco de circulo, pero esto puede ser similar a una disposición lineal (fig. 15e).
Repetición y reflexión
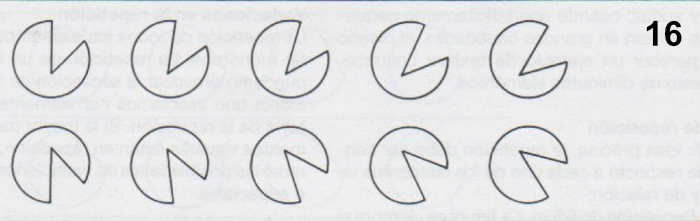
La reflexión es un caso especial de la repetición. Por reflexión entendemos que una forma es espejada, resultando una nueva forma que se parece mucho a la original, pero una va hacia la izquierda, la otra hacia la derecha y las dos nunca pueden coincidir exactamente.
La reflexión sólo es posible cuando la forma no es simétrica, ya que una forma simétrica resulta ser la misma tras la reflexión.
La rotación de una forma en cualquier dirección no puede nunca producir su forma reflejada. La forma reflejada posee un conjunto completamente distinto de rotaciones (fig. 16).
Todas las formas simétricas pueden ser divididas en dos partes: una parte componente y su reflexión. La unión de ambas partes produce la forma simétrica.
Ejercicios
Las figuras 17a, b, c, d, e y f representan el resultado de un problema simple: la repetición de módulos (círculos) de una misma forma y un mismo tamaño. No existe restricción sobre la cantidad de círculos utilizada.

Las figuras 18a, b, c, d, e, f, g y h representan los resultados de un problema más complejo: se pidió a los estudiantes que utilizaran de dos a cuatro módulos (círculos) de igual forma y tamaño, para construir un supermódulo, que luego es repetido cuatro veces para hacer un diseño. Aquí hay dos niveles de ideas. Primero, los módulos no son usados directamente para crear el diseño sino que son agrupados para convertirse en supermódulos. Segundo, los supermódulos son utilizados para el diseño final. La cantidad de círculos a utilizar en este problema no debía ser menor de ocho ni mayor de dieciséis.

Los resultados del primer problema parecen ser más agradables porque hay menos restricciones.
El segundo problema es más difícil. Sin embargo, los resultados demuestran esfuerzos especiales en la exploración de las diversas interrelaciones de formas.
Es interesante comparar los resultados de cada problema y ver cuánto puede hacer uno con la repetición de un círculo en blanco y negro. Me gustaría subrayar aquí que todos los ejercicios ilustrados fueron realizados en blanco y negro, sin tonos grises intermedios. Esto puede imponer una gran limitación, pero puede ayudar al principiante a conseguir una debida comprensión de las relaciones entre blanco y negro, que son tan esenciales en todos los trabajos de diseño que requieran la tecnología de la impresión.