La gradación es una disciplina estricta. Exige no sólo un cambio gradual, sino que ese cambio gradual sea hecho de manera ordenada. Genera ilusión óptica y crea una sensación de progresión, lo que normalmente conduce a una culminación o una serie de culminaciones.
La gradación es una experiencia visual diaria. Las cosas que están cerca de nosotros parecen grandes, y las lejanas parecen pequeñas. Si miramos desde abajo a un edificio alto, con una fachada de ventanas iguales, el cambio en tamaño de las ventanas sugiere una ley de la gradación.
Gradación de módulos
Dentro de una estructura de repetición, los módulos pueden ser utilizados en gradación. La mayor parte de los elementos visuales o de relación pueden ser utilizados en gradación, solos o combinados para obtener diversos efectos. Esto suponeque los módulos pueden tener gradación de figura, de tamaño, de color, de textura, de dirección, de oposición, de espacio y de gravedad. Sin embargo, descartaremos tres elementos: color, textura y gravedad, que trataremos más adelante. Eliminados estos, los restantes pueden reunirse en tres grupos principales: gradación en el plano, gradación espacial, y gradación en la figura.
Gradación en el plano
La gradación en el plano no afecta a la figura ni al tamaño de los módulos. La relación entre los módulos y el plano de la imagen permanece constante. Pueden distinguirse dos clases de gradación en el plano:
Rotación en el plano. Esto indica un gradual cambio de dirección de los módulos. Una figura puede ser rotada sin trasladarse en el plano de la imagen (fig. 35a).
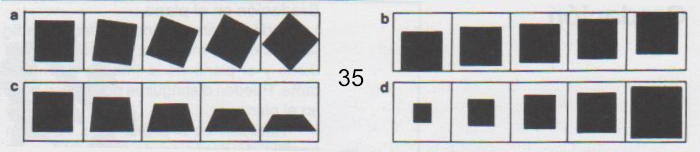
Prograsión en el plano. Esto indica un cambio gradual de posición de los módulos dentro de las subdivisiones estructurales del diseño. Los módulos pueden ascender o descender, trasladarse de un ángulo a otro de las subdivisiones, en una secuencia de movimientos regulares y graduales (fig. 35b).
Gradación espacial
La gradación espacial afecta a la figura o al tamaño de los módulos. La relación entre los módulos y el plano de la imagen nunca es constante. Pueden distinguirse dos clases de gradación espacial:
Rotación espacial. Con una separación gradual del plano de la imagen, un módulo puede ser rotado para que veamos cada vez un poco más de su borde y un poco menos de su frente. Una figura chata puede ser cada vez más estrecha hasta convertirse casi en una fina línea. La rotación espacial cambia la figura del módulo (fig. 35c).
Progresión espacial. Ésta es igual al cambio de tamaño. El aumento o la disminución en el tamaño de los módulos sugiere la progresión de los módulos en el espacio, hacia adelante o hacia atrás. Los módulos permanecen siempre paralelos al plano de la imagen, pero pueden parecer colocados muy detrás de él cuando son pequeños, o delante cuando son grandes (fig. 35d).
Gradación en la figura
Esto se refiere a la secuencia de gradaciones que resulta de un cambio real de la figura. Se sugieren dos clases comunes de gradación en la figura:
Unión o sustracción. Esto indica el cambio gradual de posiciones de los submódulos, que forman a los módulos por unión o sustracción. La figura y tamaño de cada uno de los submódulos puede asimismo experimentar al mismo tiempo racsformaciones graduales (figura 35e).
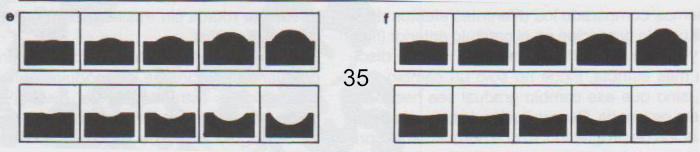
Tensión o compresión. Esto indica el cambio gradual de la figura de los módulos, por fuerzas internas o externas. La figura aparece como si fuera elástica, y resulta fácilmente afectada por cualquier ligero empuje o atracción (fig. 35f).
El camino de la gradación
Toda forma puede ser gradualmente cambiada hasta convertirse en cualquier otra. Cómo ocurre ese cambio es algo que queda determinado por el camino de gradación que se elija.
Hay múltiples caminos para la gradación. El diseñador puede escoger un camino de gradación en el plano, en el espacio, en la figura o en una combinación de ellos. El camino puede ser directo o dar un rodeo.
Por ejemplo, si deseamos cambiar un círculo en un triángulo por gradación de figura, el círculo puede ser estirado y apretado hasta ser cada vez más triangular (fig. 36a) o puede ser recortado por tres lados hasta que se convierte en un triángulo (fig. 36b). Por la gradación en el plano, el círculo puede ser elevado y seguido por un triángulo que habrá de ocupar toda la subdivisión estructural cuando el círculo haya desaparecido (fig. 36c). Por la gradación espacial el círculo puede disminuir gradualmente mientras el triángulo surge simultáneamente, primero como un punto y después como un pequeño triángulo que gradualmente se expande (fig. 36d). O el círculo puede expandirse gradualmente, más allá de los límites de la subdivisión estructural, mientras el triángulo surge (fig. 36e). Podemos así mismo considerar al círculo como la base de un cono que rota, hasta dar elevación frontal a un triángulo (fig. 36f)

Todos los caminos de la gradación así descritos son directos. Si se desea un camino más elaborado, el círculo puede ser primeramente sustituido por un cuadrado (u otra figura) antes de aproximarse a la figura del triángulo.
La velocidad de la gradación
La cantidad de pasos requeridos para que una forma cambie de una situación a otra determina la velocidad de gradación. Cuando los pasos son pocos, la velocidad es rápida, y cuando son muchos la velocidad es lenta.
La velocidad de gradación depende de los efectos que el diseñador quiera obtener. Una gradación rápida provoca saltos visuales, mientras una gradación lenta evoluciona lenta y a veces casi imperceptiblemente. La ilusión óptica es habitualmente el resultado de la gradación lenta.
Es necesario señalar que la gradación rápida debe ser utilizada con gran cautela. Si una forma cambia con demasiada rapidez, puede no existir ya una sensación de gradación, y el resultado puede ser un grupo de formas sólo vagamente relacionadas entre sí (fig. 37). En realidad no podremos cambiar efectivamente un círculo en un triángulo con menos de cinco pasos, porque normalmente ello requiere diez pasos o más.

La gradación extremadamente lenta puede aproximarse al efecto de la repetición, pero una cuidadosa disposición del dibujo puede producir resultados muy sutiles.
La velocidad de gradación puede ser cambiada en medio de una secuencia, o gradualmente acelerada o retardada para obtener efectos especiales (fig. 38).

Sin alterar la velocidad de la gradación, un camino indirecto de gradación consume normalmente meas pasos que un camino directo.
Modelos de gradación
En un modelo de gradación, importan dos factores para la construcción del dibujo: la serie de gradación, y la dirección del movimiento.
La serie de gradación queda marcada por una situación inicial y una situación final. En algunos casos, cuando el camino de la gradación no es directo sino indirecto, deben tomarse en consideración las situaciones intermedias. La cantidad de pasos entre las situaciones inicial y final determina tanto la velocidad como el alcance en la serie de gradación.
La dirección del movimiento se refiere a las orientaciones en las situaciones inicial y final y a su interrelación. Los módulos de la situación inicial pueden ser puestos en fila y procederse a lo largo, a lo ancho o en ambos sentidos, con pasos regulares hacia la situación final. También son posibles las diagonales u otras maneras de progresión. Algunos modelos típicos de gradación son:
Movimiento paralelo. Este es el más simple. Los módulos son transformados gradualmente en pasos paralelos. En el movimiento paralelo, la culminación es habitualmente una linea recta. (En la fig 39, nótese que los números representan a los diversos pasos de la gradación y que las líneas gruesas dividen la superficie en zonas, conteniendo cada zona a módulos en un mismo paso.)

Movimiento concéntrico. Esto supone que los módulos son transformados en capas concéntricas. Si la situación inicial está en una esquina del diseño, el modelo es entonces sólo parcialmente concéntrico. En el movimiento concéntrico, la culminación puede ser un punto, un cuadrado o una cruz (fig. 40).
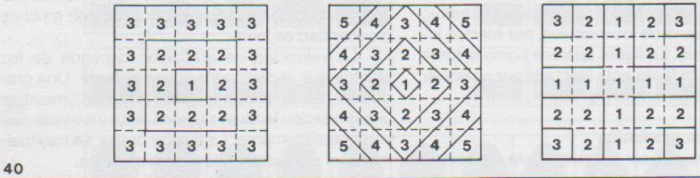
Movimiento en zigzag. Esto supone que los módulos de un mismo paso se disponen en forma de zigzag y se transforman a una misma velocidad (fig. 41)

En nuestros diagramas, sólo se muestran 25 subdivisiones estructurales (cinco hileras de cinco subdivisiones cada una). Desde luego, un modelo normal de gradación es mucho mayor, y la cantidad de pasos puede ser ampliada infinitamente. Asimismo, otros modelos pequeños de gradación pueden ser repetidos y dispuestos para formar un modelo mayor. Por ejemplo, las secciones del movimiento paralelo pueden ser reunidas para formar un diseño de gradación, a la manera que se sugiere en la figura 42.

Es esencial señalar que la gradación puede avanzar desde la situación inicial a la final y luego volver a la inicial, con la inversión de los pasos, como en el ejemplo 1-2-3-4-5-4-3-2-1. La secuencia puede ser repetida una y otra vez si es necesario, con suaves transiciones. Si se desean interrupciones regulares del modelo de gradación, ésta puede avanzar desde la situación inicial a la final y luego comenzar de nuevo, como en 1-2-3-4-5-1-2-3-4-5.
Estructura de gradación
Una estructura de gradación es similar a una estructura de repetición, excepto en que las subdivisiones estructurales no siguen siendo repetitivas sino que cambian en tamaño, figura, o ambos, en secuencia gradual y sistemática.
Casi todas las estructuras de repetición pueden ser convertidas en estructuras de gradación. Examinemos las posibilidades:
a) Cambio de tamaño y/o proporción. Las subdivisiones estructurales de un enrejado básico pueden aumentar o disminuir de tamaño (con cambio de proporción o sin él) y gradualmente de una a la siguiente. Las líneas estructurales verticales u horizontales o ambas del enrejado básico pueden ser espaciadas, con anchos gradualmente crecientes o decrecientes. La gradación puede progresar desde lo estrecho a lo ancho, y luego de lo ancho a lo estrecho, o puede ser dispuesta en cualquier secuencia rítmica (fig. 44a).

b) Cambio de dirección. Todo el conjunto de líneas estructurales horizontales o verticales o ambas, del ejemplo a), pueden ser inclinadas a cualquier dirección deseada (fig. 44b).
c) Deslizamiento. La hilera completa de subdivisiones estructurales en a) o en b) puede ser deslizada regularmente, para que una subdivisión ya no sea totalmente vecina ni encimada a la otra (fig. 44c).
d) Curvatura, quebrantamiento. Todo el conjunto de lineas verticales, u horizontales, o ambas, en a) b) y c), puede ser curvado o quebrado gradual o regularmente (fig. 44d).
e) Reflexión. Una hilera de subdivisiones estructurales que no estén en ángulo recto, como en b) y en d) , puede ser reflejada y repetida, en forma alternada y regular (fig. 44e)
f) Combinación.Las subdivisiones estructurales en a) o b) pueden ser combinadas, para formar figuras mayores o más complejas, con el efecto de gradación (fig. 44f)
g) División ulterior. Las subdivisiones estructurales en todas las estructuras de gradación pueden ser divididas en figuras más pequeñas o más complejas (fig. 44g)
h) Enrejado triangular. El enrejado triangular de una estructura de repetición, puede ser transformado en una estructura de gradación variando gradualmente el tamaño y la figura de los triángulos (fig. 44h)
i) Enrejado hexagonal. El enrejado hexagonal de una estructura de repetición, puede ser transformado en una estructura de gradación variando gradualmente el tamaño y la figura de los hexágonos (fig. 44i)
Gradación alternada
La gradación alternada aporta una complejidad poco habitual en un diseño de gradación. Significa que módulos o subdivisiones estructurales, gradualmente cambiantes, que proceden de direcciones opuestas, son entretejidos entre sí. El modo más simple de conseguir la gradación alternada es dividir la estructura (sean filas horizontales o verticales) en filas impares y pares, determinando que las filas impares observen una disciplina diferente a las pares.
Para ilustrar esto veamos la figura 43, en la que la A representa a las filas impares, y la B a las pares. Para tener una gradación alternada de los módulos, podemos disponer que los módulos de las filas A se transformen de izquierda a derecha, y los de las B en forma opuesta. Sin embargo, no es necesario que los pasos de la gradación en las filas A y B sean los mismos. Se sugieren variaciones sobre esto en las figuras 43b y c. Manipulando el grado, velocidad y dirección de la gradación podemos obtener tipos casi ilimitados de variación. Los módulos, si no son usados en gradación para ambas filas A y B, pueden ser usados en gradación en un conjunto de filas y repetidamente (en una repetición simple o alternada) en el otro conjunto.

Si los módulos están en gradación de tamaño, el espacio que queda por los módulos que disminuyen puede ser utilizado para la colocación de un conjunto de módulos en gradación inversa. Aquí los módulos originales pueden ocupar la porción central de las subdivisiones estructurales, en tanto un nuevo conjunto de módulos puede ocupar las intersecciones de las lineas estructurales (fig. 45a).

En una estructura de gradación, la gradación alternada puede obtenerse si las filas A disminuyen de manera gradual, mientras las filas B gradualmente se expanden, en forma simultánea y en la misma dirección. Esto se ilustra en la figura 45b, donde las bandas negras representan a las filas A y las bandas negra a las filas B. La ilustración puede parecer muy complicada, pero el método de construcción puede ser muy simple. El ancho conjunto de cada par de filas A y B debe permanecer constante (o en muy lenta gradación). Así, primeramente podemos dividir todo el ancho del diseño en filas combinadas de A más B, y después podemos dividir cada una de esas filas combinadas en una fila A y una fila B, procurando cuidadosamente que la A se amplíe, paso a paso, desde una fila combinada a la siguiente. Como el ancho de la fila combinada es constante, si A se expande, B se contrae automáticamente.